perceptrons(感知器)
1950s-1960s by scientist Frank Rosenblatt
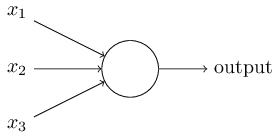
数学模型:
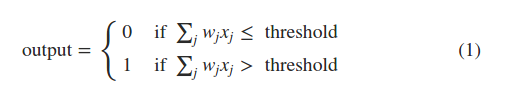
所有权重参数为w1,w2…,threshold
threshold,Dropping the threshold means you’re more willing to go to the festival.
与权重b是同一种意思,一个表示偏好的权重
感知机的输入只是0或1,输出也是0或1
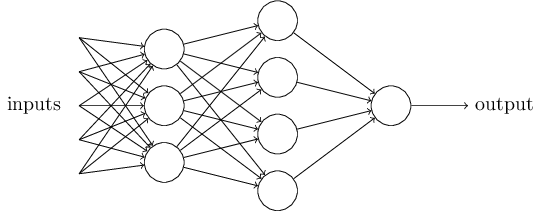
两处简化
\[\sum_{j} w_{j}x_{j} \equiv w\cdot x\] \[b \equiv -threshold\]这个bias代表的是how easy it is to get the perceptron to fire
perceptron的两种用途:
- a method for weighing evidence to make decisions
- compute simple logical functions, depend on NAND gate
perceptrons能实现与非门,但是并不是仅仅的只是实现另一种集成电路,与传统的基于与非门的集成电路不同的是,perceptrons能够通过自动调节weights和biases,来自动学习解决问题
sigmoid neurons
In fact, a small change in the weights or bias of any single perceptron in the network can sometimes cause the output of that perceptron to completely flip, say from 00 to 11. sigmoid:Sigmoid neurons are similar to perceptrons, but modified so that small changes in their weights and bias cause only a small change in their output.
perceptrons的问题是,它是阶梯变化的,不线性,微小的变化不能很好的表现出来。
sigmoid输出0-1之间的任意数,σ(w⋅x+b)
\[\sigma (z) \equiv \frac{1}{1+e^{-z}}\] \[\sigma (z) \equiv \frac{1}{1+e^{-\sum_{j}w_{j}x_{j}-b}}\]
sigmoid的一个比perceptrons不方便的地方是,output不是0或1,而是一个介于0-1之间的数,就指示一个对错的百分比而已
perceptrons和sigmoid的一些特性
- perceptrons的w b乘以任意正数c,不影响输出,sigmoid就会有影响
- 实际上sigmoid如果乘以c,且c趋于正无穷,那么sigmoid与perceptrons就一样了
MLPs:multilayer perceptrons
我们一般使用的是feedforward网络,也就是只有前进没有后退的 还有一种是Recurrent neural nets,这里包含loops,这个loops持续一段被限制的时间,不是一直循环下去,神经元本身会受到之前的激发状态的影响或者受到之前的输入的影响,Recurrent neural nets,更贴近人类的大脑
手写数字处理
output 10和4,为什么会导致识别准确率有区别?
我个人的理解是,hidden层是基于第一层输入图像的提取结果,那么这个结果是基于图像的。 而4这种方式,是基于数字的,在这层来做不合适。
在练习的部分,有提到,如果加入第三层的话,那么这层可以使用4output,因为相当于是将之前的10个数字的概率,这种基于数字的提取成另外一种数字,这样成功率应该比较高。
梯度递减
Why not try to maximize that number directly, rather than minimizing a proxy measure like the quadratic cost?
我的理解是,如果只关注结果的数字的最大化的话,那么做了些许的改变w和b,对预测结果来说,可能根本就没有变化,那么就不知道怎么继续提高分数了,这就是说这个不是一个平滑的方法。
而如果关注的是所有结果的数字的均方差的最小化的话,这是一个平滑的方法,可以进行学习。
均方差:
\[\frac{1}{2n}\sum \left \| y(x)-a \right \|^{2}\]梯度下降:
\[\Delta C \approx \bigtriangledown C\cdot \Delta v\] \[\bigtriangledown C\equiv (\frac{\partial C}{\partial v_{1}},...,\frac{\partial C}{\partial v_{m}})^{T}\] \[\Delta v=-\eta \bigtriangledown C\]stochastic gradient descent,随机梯度递减
\[\bigtriangledown C = \frac{1}{n} \sum_{x} \bigtriangledown C_{x}\]In practice, to compute the gradient ∇C we need to compute the gradients ∇Cx separately for each training input, x, and then average them, ∇C=1n∑x∇Cx
一种极端的mini-batch为1的训练,这种应用于online on-line incremental learning,就是随机梯度下降,类似于人类学习的过程
创建网络模型
从文章提供的git下载的代码,在3.5下使用需要更改几个地方
参考这篇 patch
1
2
3
4
5
6
7
8
class Network(object):
def __init__(self, sizes):
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
这里使用的是随机高斯分布(正态分布)来初始化weights和biases
测试下隐含层的神经元数量的影响:
1
2
3
4
5
6
# Epoch 29: 9384 / 10000
# train time: 0:03:17.5953027
# Epoch 29: 9418 / 10000
# train time: 0:03:28.126904
net = network.Network([784, 20, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
1
2
3
4
# Epoch 29: 9503 / 10000
# train time: 0:04:12.572446
net = network.Network([784, 30, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
1
2
3
4
# Epoch 29: 9575 / 10000
# train time: 0:05:39.106396
net = network.Network([784, 50, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
1
2
3
4
5
6
# Epoch 29: 8537 / 10000
# train time: 0:07:48.387790
# Epoch 29: 9599 / 10000
# train time: 0:07:44.628575
net = network.Network([784, 80, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
从结果看,隐含层神经元越多,测试结果一般越好,但是花费时间越多。
隐含层神经元越多,意味着从input层获取到的Feature的种类就越多,对于预测越有帮助,但是由于神经元越多,参数也就越多,所以花费时间长。
最后一次实验(对应中间层是80),结果不稳定,低的时候只有85%,可能是陷入了局部最优解,但是20的情况,我测试多次也没有出现不稳定的情况。所以看来,模型越复杂,精度可能会越好,但是越有可能不稳定(陷入局部最优、过拟合、梯度爆炸/消失等)。
测试下batch-size的影响:
1
2
3
4
# Epoch 29: 8932 / 10000
# train time: 0:04:17.280716
net = network.Network([784, 20, 10])
net.SGD(training_data, 30, 1, 3.0, test_data=test_data)
1
2
3
4
# Epoch 29: 9384 / 10000
# train time: 0:03:17.5953027
net = network.Network([784, 20, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
1
2
3
4
# Epoch 29: 9376 / 10000
# train time: 0:03:11.990982
net = network.Network([784, 20, 10])
net.SGD(training_data, 30, 20, 3.0, test_data=test_data)
1
2
3
4
# Epoch 29: 9383 / 10000
# train time: 0:02:57.594158
net = network.Network([784, 20, 10])
net.SGD(training_data, 30, 50, 3.0, test_data=test_data)
1
2
3
4
# Epoch 29: 9270 / 10000
# train time: 0:03:08.102759
net = network.Network([784, 20, 10])
net.SGD(training_data, 30, 100, 3.0, test_data=test_data)
从结果看,随着size增加,整体来看,相同epoch的时间在下降,精度也有下降趋势。所以这么看的话,size应该有个最优值,在这点上,训练时间和精度会达到最优。 另外一个现象是,在Size=1的情况下,模型没有收敛到应该有的水平。可能是由于,只根据一个样本来更新参数,整体波动比较大的原因
Toward deep learning
In the early days of AI research people hoped that the effort to build an AI would also help us understand the principles behind intelligence and, maybe, the functioning of the human brain. But perhaps the outcome will be that we end up understanding neither the brain nor how artificial intelligence works
我们人类的目的是想建立一个AI来帮助我们理解智能背后的原理,比如人类的大脑,但是讽刺的是,实际的结果是,我们造出来了AI,但是发现我们既不理解大脑也不理解AI。
MINIST数据集到图像
对于这本书里的数据集,可以在mnist_loader.py里,加入如下代码
1
2
3
4
5
6
7
8
9
10
11
def restore_image():
from PIL import Image
tr_d, va_d, te_d = load_data()
for i, img in enumerate(tr_d[0][:1]):
a = np.reshape(img, (28, 28))
new_img = Image.fromarray(a, 'L')
new_img.show()
if __name__ == "__main__":
restore_image()
fromarray的mode可以参考下表

取到的图片(这个不是数字,应该是这个图片有预处理,是从pickle里拿出来的)

对于MNIST的真正数据集,train-images-idx3-ubyte,用如下方法提取
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from PIL import Image
import numpy
import gzip
def _read32(bytestream):
dt = numpy.dtype(numpy.uint32).newbyteorder('>')
return numpy.frombuffer(bytestream.read(4), dtype=dt)[0]
def extract_images(f):
with gzip.GzipFile(fileobj=f) as bytestream:
magic = _read32(bytestream)
if magic != 2051:
raise ValueError('Invalid magic number %d in MNIST image file: %s' %
(magic, f.name))
num_images = _read32(bytestream)
rows = _read32(bytestream)
cols = _read32(bytestream)
buf = bytestream.read(rows * cols * num_images)
data = numpy.frombuffer(buf, dtype=numpy.uint8)
data = data.reshape(num_images, rows, cols, 1)
return data
with open('train-images-idx3-ubyte.gz', 'rb') as f:
images = extract_images(f)
for i in range(10):
img = Image.fromarray(numpy.reshape(images[i], (28,28)), 'L')
img.save('/home/cooli7wa/Desktop/%s.png'%i)