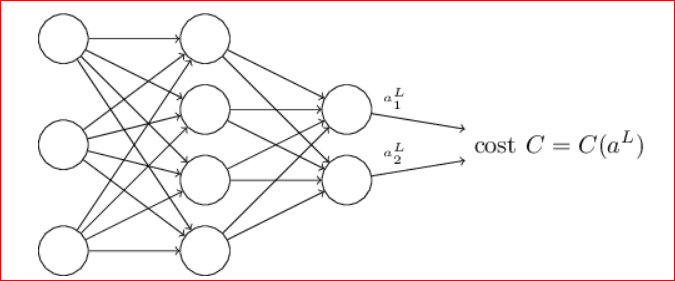
Warm up: a fast matrix-based approach to computing the output from a neural network
The two assumptions we need about the cost function
两个假设:
- \[C=\frac{1}{2n}\sum_x \left \| y(x)-a^{L}(x) \right \|^{2}\]
the cost function can be written as an average \(C=\frac{1}{n}\sum_{x}C_{x}\)over cost functions Cx for individual training examples, x.
\[C_{x}=\frac{1}{2}\left\| y-a^{L} \right\|^{2}\] the cost is that it can be written as a function of the outputs from the neural network
\[C_{x}=\frac{1}{2}\left \| y-a^{L}\right \|^{2}=\frac{1}{2}\sum_{j}(y_{j}-a_{L}^{j})^{2}\]![]()
总体的Cost,依赖于所有的输入x(对于)和每个输入x的所有的output a
The Hadamard product, s⊙t
1
2
3
4
5
# 与矩阵乘法不同
# 这个的写法是
a*b
# 矩阵乘法的写法是
np.dot(a, b)
The four fundamental equations behind backpropagation
一些基础点:
- \[\delta_{j}^{l}\equiv \frac{\partial C}{\partial z_{j}^{l}}\]
the error in the \(j_{th}\) neuron in the \(l_{th}\) layer add a little\(\bigtriangleup z_{j}^{l}\), so output \(\sigma(z_{j}^{l}) \rightarrow\sigma(z_{j}^{l}+\bigtriangleup z_{j}^{l})\)
最终的output为\(\frac{\partial C}{\partial z_{j}^{l}}\bigtriangleup z_{j}^{l}\)
- \(z_{j}^{L}\)并不是神经元输出,\(\sigma(z_{j}^{L})\)才是
第一个基础公式(An equation for the error in the output layer):
下面的推导是针对output层来说
\[\delta_{j}^{L}=\frac{\partial C}{\partial z_{j}^{L}}\rightarrow \sum_{k}\frac{\partial C}{\partial a_{k}^{L}}\frac{\partial a_{k}^{L}}{\partial z_{j}^{L}}\rightarrow \frac{\partial C}{\partial a_{j}^{L}}\frac{\partial a_{j}^{L}}{\partial z_{j}^{L}}\rightarrow \frac{\partial C}{\partial a_{j}^{L}}\sigma'(z_{j}^{L})\]Of course, the output activation \(a_{k}^{L}\) of the \(k^{th}\) neuron depends only on the weighted input \(z_{j}^{L}\) for the \(j^{th}\) neuron when k=j.
现在讨论的是输出层的状态,所以\(a_{j}\)(也就是\(\sigma\))只与\(z_{j}\)有关。
\[C=\frac{1}{2}\sum_{j}(y_{j}-a_{j}^{L})^{2} \rightarrow \partial C/\partial a_{j}^{L}=(a_{j}^{L}-y_{j})\] \[(y_{j}-a_{j}^{L})(y_{j}-a_{j}^{L})'= (a_{j}^{L}-y_{j})\] \[\delta^{L}=\bigtriangledown_{a}C\odot \sigma '(z^{L})\]当loss是均方差的时候,可以化简为下面这个
\[\delta^{L}=(a^{L}-y)\odot \sigma '(z^{L})\]这里的⊙需要注意下,这个不是一般的矩阵乘法
第二个公式(An equation for the error δlδl in terms of the error in the next layer)
\[\delta^{L}=((w^{l+1})^{T}\delta ^{l+1})\odot \sigma '(z^{L})\]推导的过程文章下面介绍很详细
第三个公式(An equation for the rate of change of the cost with respect to any bias in the network)
\[\frac{\partial C}{\partial b^l_j}=\delta _j^l\]第四个公式(An equation for the rate of change of the cost with respect to any weight in the network)
\[\frac{\partial C}{\partial w_{jk}^{l}}=a_{k}^{l-1}\delta_{j}^{l}\rightarrow \frac{\partial C}{\partial w}=a_{in}\delta _{out}\]A nice consequence of Equation (32) is that when the activation \(a_{in}\) is small, \(a_{in}\)≈0, the gradient term ∂C/∂w will also tend to be small.
In this case, we’ll say the weight learns slowly, meaning that it’s not changing much during gradient descent.
当\(a_{in}\)很小的时候,参数的学习很慢
so the lesson is that a weight in the final layer will learn slowly if the output neuron is either low activation (≈0) or high activation (≈1). In this case it’s common to say the output neuron has saturated and, as a result, the weight has stopped learning (or is learning slowly).
当使用sigmoid激活函数的时候,如果神经元的输出接近0或1的时候,学习也很慢
Summing up, we’ve learnt that a weight will learn slowly if either the input neuron is low-activation, or if the output neuron has saturated, i.e., is either high- or low-activation.


Fully matrix-based approach to backpropagation over a mini-batch
这是一种提升速度的方式,在tensorflow里面,应该已经在使用了。
可以试试在tensorflow里面,这个速度快多少?
写了一份代码,跑起来使用GPU+tensorflow,速度也没有提升太多(比如10倍)
0:04:00.804773 原来的
0:02:45.739480 现在的
代码:mnist_tensor_mine/src/tensor_network.py
In what sense is backpropagation a fast algorithm?
如之前视频里讲解的一样,反向传播,将需要计算量大为缩减,与正向传播基本计算量相等。
但是这个是有前提的,就是现在计算的是,大量的输入,一个输出(比如就是是否符合预期),反向传播是适用的,但是有的模型是,一个输入,大量的输出,这时,正向传播才是合适的
Backpropagation: the big picture
转换成tensorflow,之后的测试情况
有一些准备过程:
- 参照这篇文档来做,数据格式需要处理
Batch_size的影响
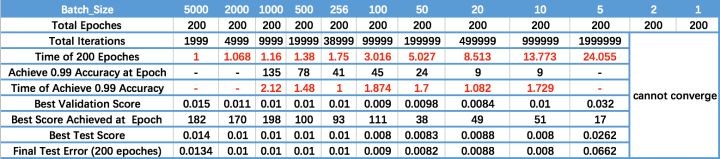
- Batch_Size 太小,算法在 200 epoches 内不收敛。
- 随着 Batch_Size 增大,处理相同数据量的速度越快。
- 随着 Batch_Size 增大,达到相同精度所需要的 epoch 数量越来越多。
- 由于上述两种因素的矛盾, Batch_Size 增大到某个时候,达到时间上的最优。
- 由于最终收敛精度会陷入不同的局部极值,因此 Batch_Size 增大到某些时候,达到最终收敛精度上的最优。