Neural Networks And Deep Learning Chap3

原文地址

• a better choice of cost function, known as the cross-entropy cost function
• four so-called “regularization” methods (L1 and L2 regularization, dropout, and artificial expansion of the training data)，L1 L2正则化、dropout、虚假扩展数据
• a better method for initializing the weights in the network
• a set of heuristics to help choose good hyper-parameters for the network

The philosophy is that the best entree to the plethora of available techniques is in-depth study of a few of the most important.

对现在过多的技术，最好的方式了，深入研究几个最重要的技术

The cross-entropy cost function

loss函数是均方差，激活函数是sigmoid的时候

\[\frac{\partial C}{\partial w}=(a-y)\sigma'(z)x=a\sigma'(z)\] \[\frac{\partial C}{\partial b}=(a-y)\sigma'(z)=a\sigma'(z)\]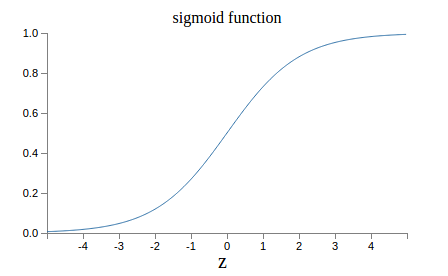

当output接近0或1的时候，函数很平坦，梯度就很小，学习很慢

Introducing the cross-entropy cost function

\[c=-\frac{1}{n}\sum_{x}[ylna+(1-y)ln(1-a)]\]

什么样的交叉熵可以做为损失函数？

• 函数结果是非负的
• 当实际输出结果和期待的结果接近的时候，函数输出应该接近0 （假设a=y=0或a=y=1）

从上面这两点看，交叉熵是合适的

交叉熵为什么可以防止训练速度慢？

\[\frac{\partial C}{\partial w_{j}}=\frac{1}{n}\sum_{x}x_{j}(\sigma(z)-y)\] \[\frac{\partial C}{\partial b}=\frac{1}{n}\sum_{x}(\sigma(z)-y)\]

\(\sigma(z)-y\)就是error，所以error越大，学习速率就越大，这个符合人学习的特点。

另外交叉熵的cost/epoch曲线，更加陡峭

什么时候使用交叉熵？

如果激活函数是sigmoid的话，那么损失函数就应该是交叉熵，因为可以放置训练过慢的问题。对于其他的激活函数，并没说。

\[C=-\frac{1}{n}\sum_{x}\sum_{j}[y_{j}lna^{L}_{j}+(1-y_{j})ln(1-a^{L}_{j})]\]

这个公式和别的地方的函数里用的不一样，这里是两项相加，都当成了概率

均方差并不是总是会造成学习速率慢的问题，当最后一层的神经元是线性的（也就是没有sigmoid的激活函数），这时的偏导数就不会有这个问题。

所以来看，学习速率慢的问题，貌似只在sigmoid配合均方差的时候出现。所以均方差也不是用在哪里都不合适。

Using the cross-entropy to classify MNIST digits

cross-entropy对比quadratic cost

原文
784, 30, 10
30, 10，0.5
    95.42 -> 95.49

784, 100, 10
30, 10，0.5
    96.59 -> 96.82
error: 3.41 -> 3.18，下降了1/12，下降很多了

自己
784, 30, 10
30, 10，0.5
    95.19 -> 95.36

784, 100, 10
30, 10，0.5
    96.51 -> 96.63

需要注意的是，这里没有仔细调参，所以通过这个结果直接说，cross-entropy比quadratic要好，不严谨。不过作者也说，实际上确实要好

为什么关注损失函数？

the more important reason is that neuron saturation is an important problem in neural nets

主要原因是，神经元的饱和度是一个特别重要的问题，这里值得花力气来研究，这个也应该是深度学习的主要方面。

What does the cross-entropy mean? Where does it come from?

\[\sigma'(z)=\sigma(z)(1-\sigma(z))\]

这个是从\(\sigma(z)=\frac{1}{1+e^{-z}}\)求导而来

\[\frac{\partial C}{\partial w_{j}}=\frac{1}{n}\sum_{x}x_{j}(\sigma(z)-y)\]

从上面的公式可以看出来，x也是影响学习速率的一个主要因素，当x接近0的时候，速率也很慢

Softmax

softmax可以用来解决学习速率慢的问题？

这里的softmax并不是我理解的那样，只是一个归一化的处理过程。文章这里的softmax是作为一个激活函数来用的，类似于sigmoid。

当cost为\(c\equiv -lna^{L}_{y}\)（这个叫做log-likelihood cost）时，可以推到出来下面的公式：

\[\frac{\partial C}{\partial b^{L}_{j}}=a^{L}_{j}-y_{j}\] \[\frac{\partial C}{\partial w^{L}_{jk}}=a^{L-1}_{k}(a^{L}_{j}-y_{j})\]

从这里可以看出来，这个与sigmoid+crossentropy是一样的

所以说这个也解决了速率慢的问题。

w的证明过程如下：

\[\frac{\partial C}{\partial z^{l}_{j}}=\frac{\partial C}{\partial a}\frac{\partial a}{\partial z^{l}_{j}}=-\frac{1}{a^{l}_{j}}\frac{e^{z^{j}_{l}}\sum-(e^{z^{j}_{l}})^{2}}{\sum^{2}}=..=\frac{e^{z^{j}_{l}}-\sum}{\sum}=a^{l}_{j}-1=a^{l}_{j}-y_{j}\]

log-likelihood cost，可以作为损失函数，因为还是那么几点

• 非负的，当\(a^{L}_{y}\)为1的时候，cost就是0，也就是第y个神经元的输出与期待1相符，没有偏差
• 当实际输出结果和期待的结果接近的时候，函数输出应该接近0
• 当不接近的时候，输出应该远离0
• 注意\(c\equiv -lna^{L}_{y}\)这里的y，是指输出层第几个神经元的输出，比如对于mnist，如果这里要计算图像与7的偏差，那么这里的y就是7

The fact that a softmax layer outputs a probability distribution is rather pleasing. In many problems it’s convenient to be able to interpret the output activation \(a^{L}_{j}\) as the network’s estimate of the probability that the correct output is j.

softmax的输出可以理解为是一个概率分布，是\(a^{L}_{j}\)是j的概率。

a network with a sigmoid output layer, the output activations \(a^{L}_{j}\) won’t always sum to 1.

sigmoid的输出，并不是相加总为1

You can think of softmax as a way of rescaling the \(z^{L}_{j}\), and then squishing them together to form a probability distribution.

sigmoid使z成为一个概率分布

现在知道了两种组合：

• sigmoid + crossentropy
• softmax + log-likelihood

Overfitting and regularization

这里的测试，是按照下面的比例来做的，train_data只有1000，因为数据少了，epoch设置为了400，其他没变

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2 
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) 
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data,
... monitor_evaluation_accuracy=True, monitor_training_cost=True)

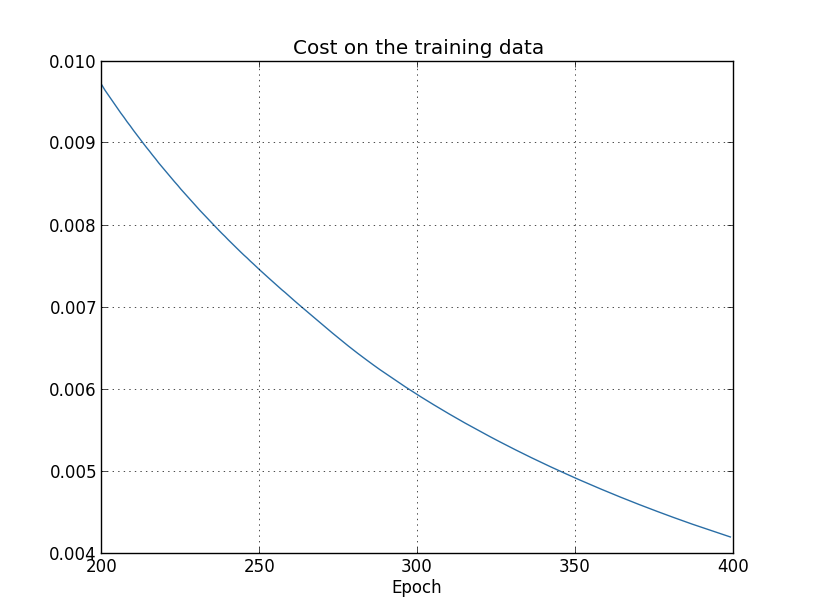
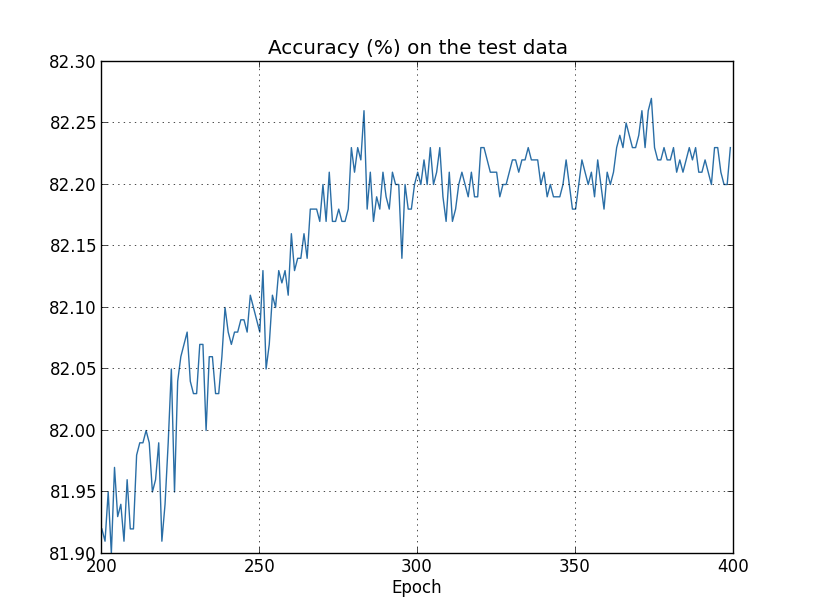
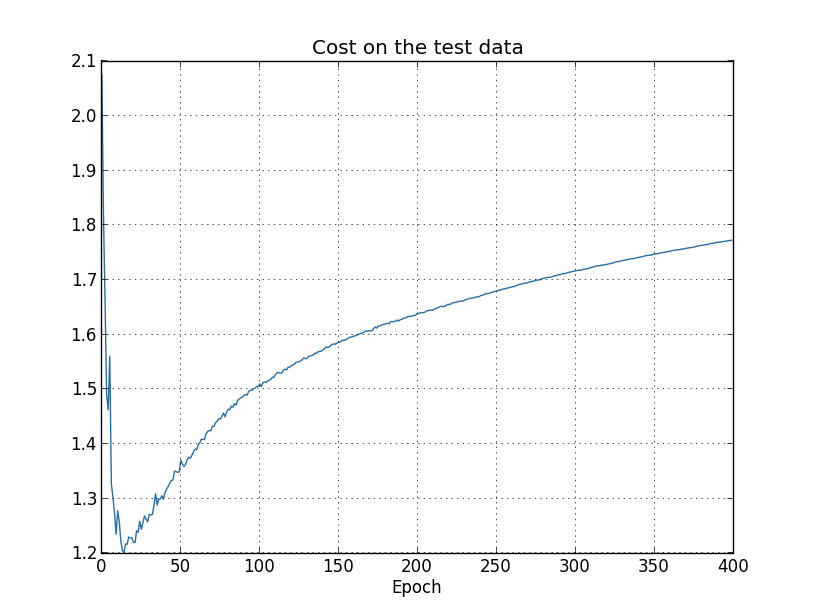
这里有个问题

• 从accuracy来看，overfitting是从280epoch开始的
• 从cost on test data来看，overfitting是从15epoch开始的

那么哪个才是真正的overfitting起始点？

From a practical point of view, what we really care about is improving classification accuracy on the test data, while the cost on the test data is no more than a proxy for classification accuracy. And so it makes most sense to regard epoch 280 as the point beyond which overfitting is dominating learning in our neural network.

文中的观点是，280才是，但是这个观点有点草率，后面作者也会说

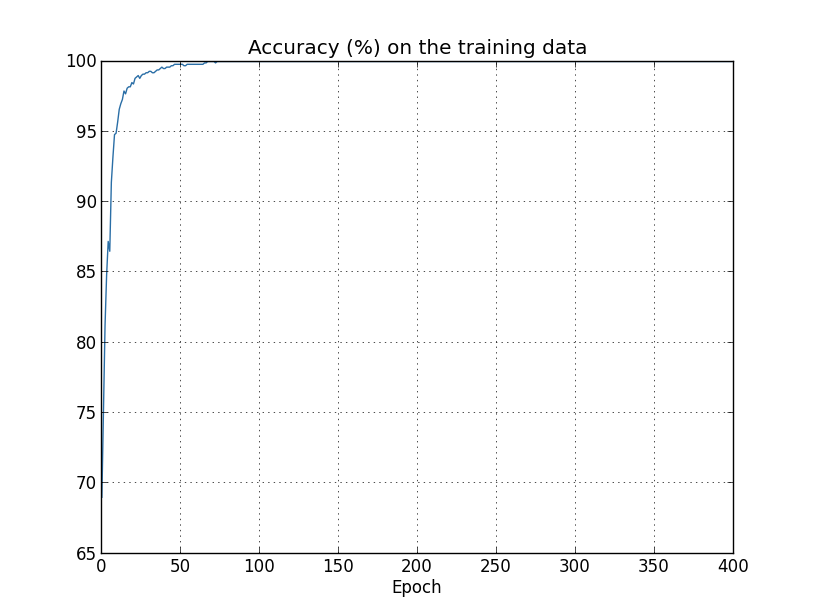
这里正确率是100%，那就是说，网络记住了整个训练数据，而不是理解

避免overfitting的方式：

• 时刻关注在测试集（验证集）上的正确率，如果正确率停止增长，那么就停止训练。 但是严格来说，这个并不能真正的识别overfitting，因为有时是训练集和测试集同时停止了增长。但这个应该可以防止overfitting的发生。 （这里作者也在说，判断何时算是overfitting，这个应该谨慎，因为训练过程中，有时就会发生一段时间内正确率不上升的情况，这种类似平坦的地形，但是过后，就又会开始上升。）
• 增大数据量
• 正则化（后面会说）

这里关于数据集的划分方面，是这样定的

• train
• validation，在这个数据集上来测试调整过的超参，并选择其他的超参
• test，在这个数据集上来最终测试网络，这个算是最终的测试集

Regularization

减少网络的尺寸，也是一种减少过拟合的方式，但是这个我们一般不会采用，但是这是一种思路，要知道。

weight decay or L2 regularization，是一回事

交叉熵的L2：

\[C=-\frac{1}{n}\sum_{xj}[y_{j}lna^{L}_{j}+(1-y_{j})ln(1-a^{L}_{j})]+\frac{\lambda}{2n}\sum_{w}w^{2}\]

\(\frac{\lambda}{2n}\)，\(\lambda>0\)，叫做正则参数，n是样本的数量，后面会讨论如何选择正则参数

注意这里只有w，没有b，原因如下：

• Empirically, doing this often doesn’t change the results very much
• At the same time, allowing large biases gives our networks more flexibility in behaviour
• in particular, large biases make it easier for neurons to saturate, which is sometimes desirable，饱和是我们希望的？

均方差的L2：

\[C=\frac{1}{2n}\sum_{x}\left \|y-a^{L}\right \|^{2}+\frac{\lambda}{2n}\sum_{w}w^{2}\]

通用形式的L2：

\[C=C_{0}+\frac{\lambda}{2n}\sum_{w}w^{2}\]

Large weights will only be allowed if they considerably improve the first part of the cost function. ？？这里不明白

\[\frac{\partial C}{\partial w}=\frac{\partial C_{0}}{\partial w}+\frac{\lambda}{n}w\] \[\frac{\partial C}{\partial b}=\frac{\partial C_{0}}{\partial b}\] \[b\rightarrow b-\eta \frac{\partial C_{0}}{\partial b}\] \[w\rightarrow w-\eta \frac{\partial C_{0}}{\partial w}-\frac{\eta\lambda }{n}w=(1-\frac{\eta \lambda }{n})w-\eta \frac{\partial C_{0}}{\partial w}\]

后来的测试里面，使用正则都要好过没使用正则的结果

为什么L2正则可以减少overfitting，而且得到更好的结果？

• 对于L2正则来说，L2减小了w，w越小，每次迭代w的变化就越小，这样即使样本少，数据不均衡，平均不完全，也可以减小陷入到局部最优解的可能性
• 如果样本多的话，那么学习的目标就多，那么取平均值之后，陷入到少样本的局部最优解里的可能性就小，这是为什么多样本，可以减小overfitting
• 如果样本多，而且使用L2，那么效果自然就更好

Why does regularization help reduce overfitting?

One point of view is to say that in science we should go with the simpler explanation, unless compelled not to.

正则可以抵抗noise

下面的两个例子，再说的是，正则产生的帮助，是无法简单解释。。

A network with 100 hidden neurons has nearly 80,000 parameters. We have only 50,000 images in our training data. It’s like trying to fit an 80,000th degree polynomial to 50,000 data points. By all rights, our network should overfit terribly. And yet, as we saw earlier, such a network actually does a pretty good job generalizing.

我们的输入是50000个点，模型的参数缺有80000个，所以这样看的话，应该会过拟合严重，但是实验的结果却是一个好的结果，这里是一个无法解释的地方。

“the dynamics of gradient descent learning in multilayer nets has a ‘self-regularization’ effect”

梯度下降，好像自带正则效果

Other techniques for regularization

• L1 regularization

\[C=C_{0}+\frac{\lambda}{n}\sum_{w}\left | w \right |\]

\(\frac{\partial C}{\partial w}=\frac{\partial C_{0}}{\partial w}+\frac{\lambda}{n}sgn(w)\), sgn(w), w>0:+1 w<0:-1

\[w\rightarrow w'=w-\frac{\eta \lambda }{n}sgn(w)-\eta \frac{\partial C_{0}}{\partial w}\]

L0：计算非零个数，用于产生稀疏性，但是在实际研究中很少用，因为L0范数很难优化求解，是一个NP-hard问题，因此更多情况下我们是使用L1范数
L1：计算绝对值之和，用以产生稀疏性，因为它是L0范式的一个最优凸近似，容易优化求解
L2：计算平方和再取平均数，L2范数更多是防止过拟合，并且让优化求解变得稳定很快速（这是因为加入了L2范式之后，满足了强凸）。

L1和L2的区别是，L1使用的固定值的衰减，而L2使用的是w的比例衰减，所以在w比较大的时候，L2衰减更快，在w小的时候，L1衰减更快。

The net result is that L1 regularization tends to concentrate the weight of the network in a relatively small number of high-importance connections, while the other weights are driven toward zero.

L1倾向于保存比较大的w，而其他的w趋于0。

L1产生稀疏性，因为很多小w，被衰减为0。

稀疏性的好处是可解释性，即根据非零系数所对应的基的实际意义来解释模型的实际意义，而且可以缩减数据量

另外L1，需要注意w=0的点，因为

\[\left | w \right |\]

在这点是不可导的，在实际使用的时候，需要额外处理。

• dropout

每个batch是一个循环

1. 恢复之前dropout的神经元
2. 随机砍掉一半的神经元
3. 正向反向传播，更新参数

有一个地方需要注意，由于实际算出来的参数是只有一半的中间神经元，当做评估的时候，需要使用所有的神经元，所以训练时候得到的参数，应该除以2.

为什么dropout可以生效？

The reason is that the different networks may overfit in different ways, and averaging may help eliminate that kind of overfitting.

And so the dropout procedure is like averaging the effects of a very large number of different networks. The different networks will overfit in different ways, and so, hopefully, the net effect of dropout will be to reduce overfitting.

因为dropout相当于产生了很多不同模型的网络，每个网络都可能过拟合成不同的方式，而dropout平均化了这些方式，所以可以生效。

Dropout has been especially useful in training large, deep networks, where the problem of overfitting is often acute.

当网络大且深的时候，防止过拟合就越来越重要

• artificially increasing the training set size

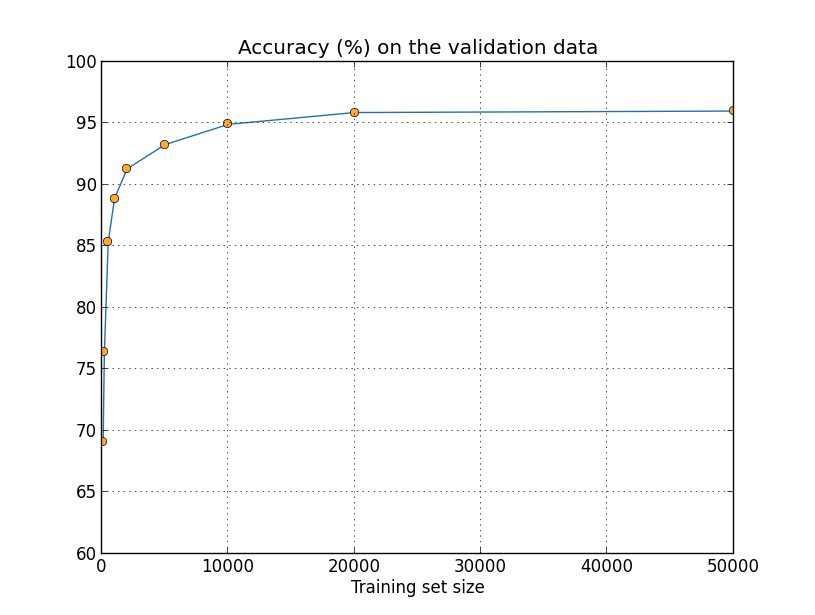
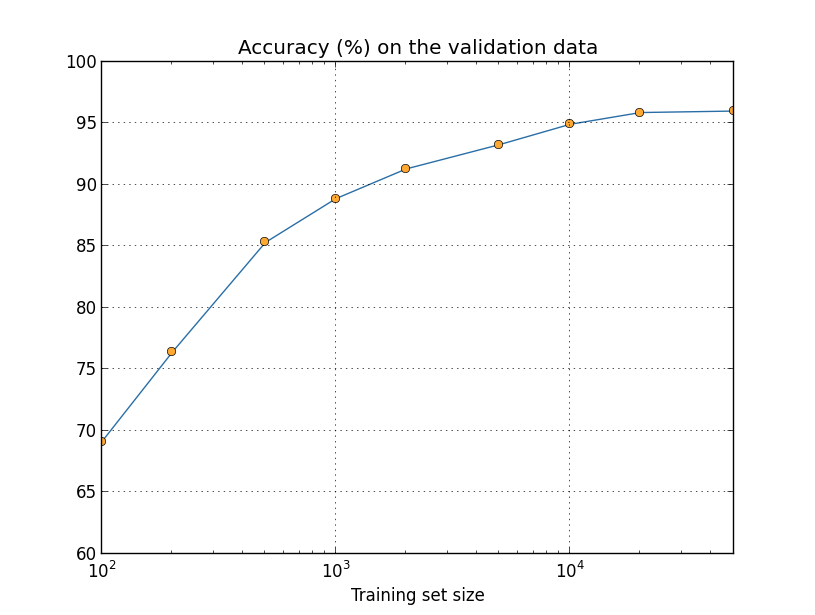
两个不同的算法AB，可能发生的情况是，在数据集X上，A要好，在数据集Y上，B要好，所以如果有人问，是A好还是B好，那么应该反问，你选择哪个数据集？

手写数字识别

• 基础情况：98.4
• 加入一些基础扩展，比如旋转等：98.9
• 加入一个特殊的随机的晃动（模拟手写时候的晃动）：99.3

It’s fine to look for better algorithms, but make sure you’re not focusing on better algorithms to the exclusion of easy wins getting more or better training data.

寻找好的算法，也找寻找好的数据，一个好的数据，会使达到好成绩变得简单地多。

Weight initialization

\[z=\sum_{j}w_{j}x_{j}+b\]

这个公式，当1000个input，其中500个1,500个0，w和b都采用标准正态分布来初始化，那么， z符合N(0,501)的正态分布，这个正态分布就很平，导致的结果就是，z远大于1或者远小于-1的可能性很大，就是|z|取大值的可能性很大。

这时候，如果激活函数是sigmoid的话，那么\(\sigma(z)\)就很接近1，也就是饱和了，学习速率就很低（这个应该是说的是sigmoid的情况了）。

We addressed that earlier problem with a clever choice of cost function. Unfortunately, while that helped with saturated output neurons, it does nothing at all for the problem with saturated hidden neurons.

之前的更换损失函数从均方差到交叉熵，只是解决了输出层的饱和问题，没法解决中间层的饱和问题！

如何避免这个问题呢？

可以在初始化的时候，将标准正态分布，换成\(N(0,1/\sqrt{n_{in}})\)，b还是使用的标准正态分布，因为这个有人实验证明过，没有啥影响。

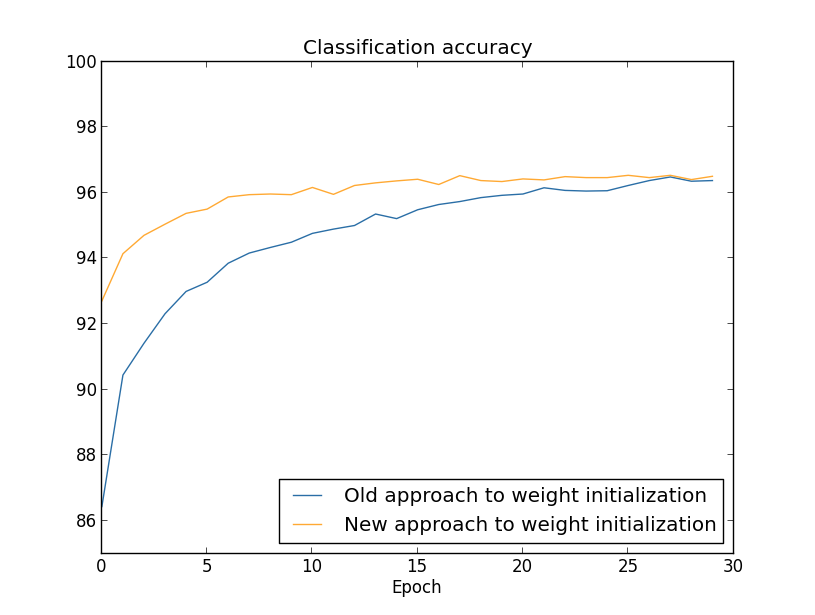
实验结果，可以看出来，虽然最后结果一样，但是上升速度要快，并且提前达到最后的96精度

However, in Chapter 4 we’ll see examples of neural networks where the long-run behaviour is significantly better with the 1/nin‾‾‾√1/nin weight initialization. Thus it’s not only the speed of learning which is improved, it’s sometimes also the final performance.

初始化的值，并非只是影响学习速率，也会影响到最终的结果。

L2 regularization sometimes automatically gives us something similar to the new approach to weight initialization.

L2正则和优化初始化值的方式，比较相似，都是减小参数

Handwriting recognition revisited: the code

save和load使用的是json，也可以使用pickle 作者的意思是使用json，可以方便在以后更改代码之后，load数据 但是实际上pickle也可以做到这点，以前看过类似的做法

How to choose a neural network’s hyper-parameters?

开启monitor，这个很重要

• Broad strategy
  • 可以从10个分类，减少到两个分类，比如先尝试分类0和1，这样会减少时间
  • 可以减少网络层数，也可以减少时间，后续再增加层数
  • 可以减少训练的数据量，虽然这个可能造成overfitting等，但是现在不是避免这个的时候，现在主要是想测试参数。 前期的时候，能够快速回馈是最重要的事，模型一定要简单，数据也要简单，要记住。
• Learning rate

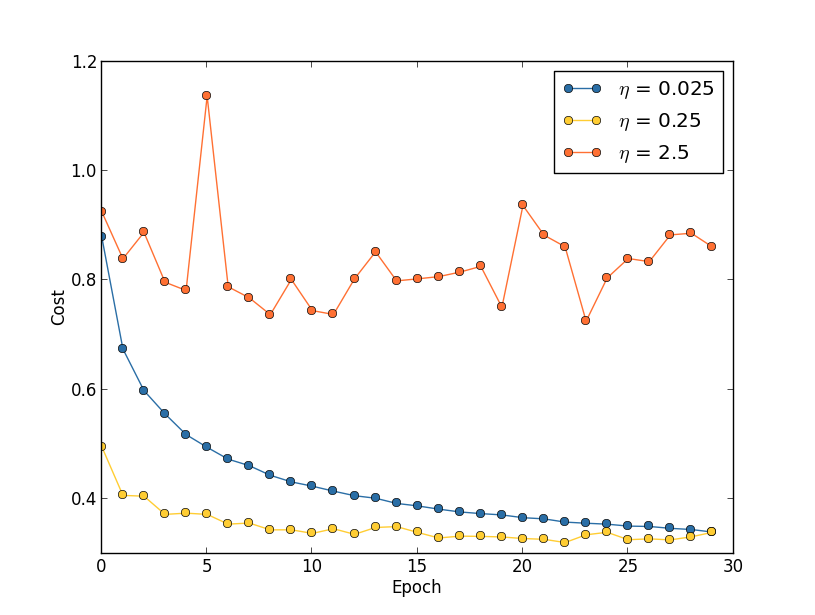
0.25在最小点附近有震荡，0.025又太慢了

最好的办法是比如前20epochs使用0.25，后面10个epochs使用0.025

如何一步步选择rate？

首先rate，按照作者的经验是，与训练本身的速率有关，所以作者用的是cost作为判断标准，而其他的参数，比如mini-batch，层数等等，都是用的valiadate数据集的准确率作为判断标准。

1. 先选择一个经验值，比如0.01或者0.1
2. 找到上限值。看训练的前几个epoch，如果cost在下降，那么尝试加大rate，如果上升或者震动，那么就减少rate，这样可以找到一个上限值
3. 用上限值训练，观察图，如果在最低点附近震荡的话，那么就尝试减少一点rate
4. 直到找到一个既迅速又不震荡的rate

• Use early stopping to determine the number of training epochs

在测试集或者验证集上，如果一段时间正确率不上升，就停止训练。

这个可以简化epoch的选择，并且减少overfitting。

但是在前期，作者并不建议使用这种方案，作者是希望overfitting发生，然后使用正则来处理。

如何实现？

A better rule is to terminate if the best classification accuracy doesn’t improve for quite some time.

比如，从no-improvement-in-ten开始，需要知道的是，有时模型就是会平坦一段时间，这段时间内没有正确率上升，所以这个判断的标准，要根据实际情况来定。

• Learning rate schedule

学习速率递减，怎么递减？

一种方法是，当验证集的正确率下降的时候开始减小学习速率，可以按照 a factor of two or ten（也就是减小到原来的1/2或者1/10），直到减小到1/1024（or 1/1000），就停止减小。

需要知道的是，跟early stop一样，这个也增加了额外的参数，也就是增加了需要调整的地方，在前期的时候，没必要这么做，后期追求分数的时候，再这么做。

• The regularization parameter, λ

最开始的时候，λ=0.0即可，先调整η ,η 调整到一个合适的数值之后，开始调整 λ，可以按照10倍的速率增加或者减少，当确定好 λ之后，再回过头去继续调整η。

• How I selected hyper-parameters earlier in this book
• Mini-batch size

online_learning(batch为1)，会导致梯度有问题，但是这个不是一个很要紧的事，因为如下：

It’s as though you are trying to get to the North Magnetic Pole, but have a wonky compass that’s 10-20 degrees off each time you look at it. Provided you stop to check the compass frequently, and the compass gets the direction right on average, you’ll end up at the North Magnetic Pole just fine.

那是不是online_learning，是最好的选择了呢？因为既可以达到最优点，也频繁得更新参数，不是很好？但是有一点需要注意，因为batch size =1，那么10000个样本的epoch就必须循环10000次，而且没有用到矩阵计算的优势，这样就很慢，学习时间就会长。

如果batch size太大，那么参数更新就不够频繁，也不好。所以需要综合起来考虑。

所幸的是，batch_size与其他参数的没啥关系，所以只需定下其他参数，单独优化这个就好。

所以应该是在最优点一致的情况下，选择一个最大的batch size，使训练时间最短。

• Automated techniques

自动优化参数

• Summing up

有一些paper介绍了如何选择参数

选择参数这个问题，现在也没有解决，没有一个统一的方式

So your goal should be to develop a workflow that enables you to quickly do a pretty good job on the optimization, while leaving you the flexibility to try more detailed optimizations, if that’s important.

所以就是定下一个自己的流程，这个流程应该可以做出一个比较好的参数，然后再细致得调整。

Other techniques

Variations on stochastic gradient descent（变种随机梯度下降）

• Hessian technique Intuitively, the advantage Hessian optimization has is that it incorporates not just information about the gradient, but also information about how the gradient is changing.
• momentum

Other approaches to minimizing the cost function

As you go deeper into neural networks it’s worth digging into the other techniques, understanding how they work, their strengths and weaknesses, and how to apply them in practice.

Other models of artificial neuron

• tanh，具体公式不记录了，这个与sigmoid类似，只是output从0,1到了-1,1 一般认为tanh要比sigmoid要好，因为sigmoid由于是非负的，所以对一个神经元来说，所有的w同时上升或者下降，这个不太贴合实际。而tanh，就可以避免这个问题。 但是现在实验起来，tanh比sigmoid又没有多少进步或者进步很小。
• rectified linear neuron（就是relu） image recognition上面用的比较多，并且比较有效。这种激活函数，没有sigmoid类似函数的饱和问题。

network2 code

• 增加了cross-entropy
• 增加了权重衰减
• 增加了Save load
• 增加了monitor

  # 均方差
  0.5*np.linalg.norm(a-y)**2
  # 交叉熵
  np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) # nan_to_num，如果是nan则换为0，如果是infinite，则换为inf