Neural Networks And Deep Learning Chap4

原文地址

Almost any process you can imagine can be thought of as function computation. 

Of course, just because we know a neural network exists that can (say) translate Chinese text into English, that doesn’t mean we have good techniques for constructing or even recognizing such a network.

Two caveats

• First, this doesn’t mean that a network can be used to exactly compute any function.Rather, we can get an approximation that is as good as we want. By increasing the number of hidden neurons we can improve the approximation.

  准确的拟合无法做到，但是通过提升中间层神经元的数量，足够精度的拟合总是可以做到

• The second caveat is that the class of functions which can be approximated in the way described are the continuous functions.

  因为神经网络是根据输入计算的连续函数，所以对于非连续的函数，不能很好得拟合

  However, even if the function we’d really like to compute is discontinuous, it’s often the case that a continuous approximation is good enough.  即使函数不是连续的，神经网络计算出的连续的拟合，经常也是足够好的

Summing up, a more precise statement of the universality theorem is that neural networks with a single hidden layer can be used to approximate any continuous function to any desired precision.

Universality with one input and one output

\[\sigma(wx+b), \ \sigma(z)=1/(1+e^{z})\]

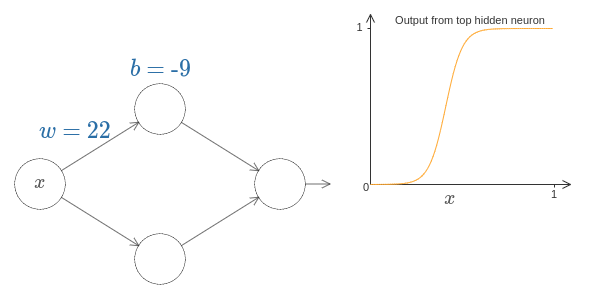
这个图形的特点是，w控制图形的“胖瘦”，w和b共同控制图形的中心点位置（s=-b/w）。

如果只改变b，那么图形平移。

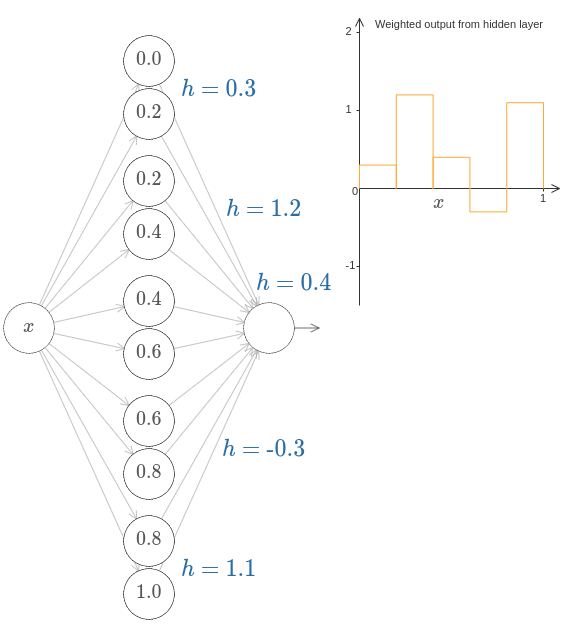
这张图可以看出来，中间层的，每两个神经元构成了输出图像的一个矩形，这两个神经元的s（圆内数值）相差的值，就是矩形的宽度，h控制的矩形的高度，这样就可以拟合任意图形，这类似于积分。

Many input variables

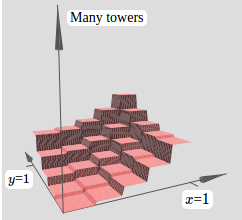
类似于平面的情况

Extension beyond sigmoid neurons

作者这里介绍了另外一种样式的激活函数，图形如下：

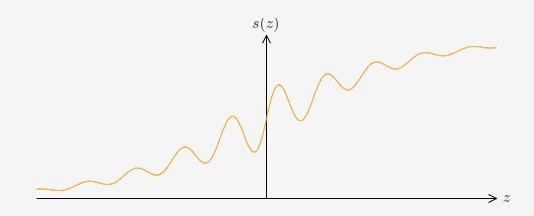
对应的输出图形为：

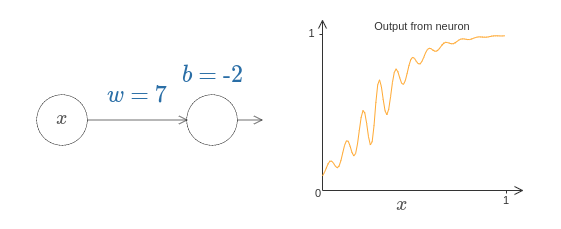
这种激活函数，通过调节w，也可以达到step function，所以这种来拟合也没有问题。

但是自己在实验的时候，没有特殊操作过w和b（比如，按照作者所言，w需要非常一个数），也可以拟合得很好：

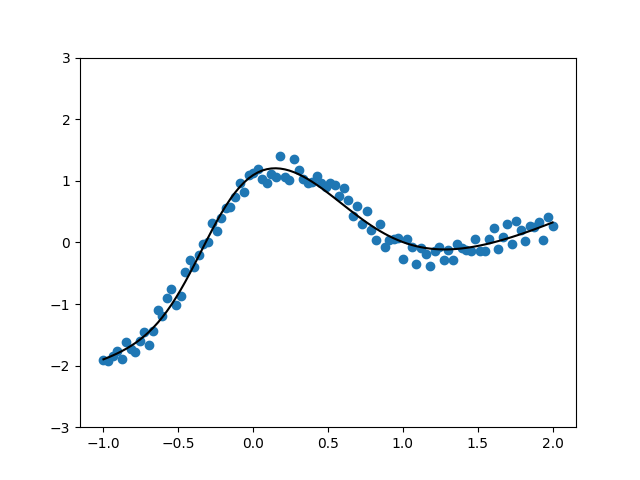
而且将第一层的W打印出来，也并不是很大的数：

[[ 1.43674046e-01 -1.20247200e-01 -7.25370944e-02  1.19405329e-01
  -1.38694555e-01 -4.56957966e-02 -6.28167158e-03  1.19999368e-02
  -5.14546297e-02 -2.37682499e-02  1.44006923e-01  1.42787874e-01
  ...]]

所以作者所说的step function的情况，应该是比较好理解的一种情况，但是实际上神经网络不需要严格限制w和b，也可以通过别的方式，来拟合多项式

像relu这种线性激活函数，是无法拟合多项式的，因为无法提供非线性的特征

Fixing up the step functions

在之前，都假设是一个完美的step function，但是实际上，不会很完美，如作者所画，这里面由failure window

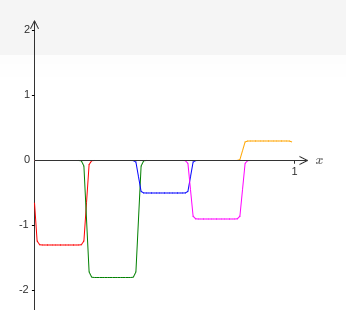
这种window可以通过手段减小，但是不会消失，虽然不会消失，但是对拟合的影响可以控制。

这里还是上面的问题，在自己实验里，这里的step function并不存在，说明神经网络并不是一定通过step这种方式来进行的拟合。

Conclusion

Although the result isn’t directly useful in constructing networks, it’s important because it takes off the table the question of whether any particular function is computable using a neural network. The answer to that question is always “yes”. So the right question to ask is not whether any particular function is computable, but rather what’s a good way to compute the function.

universality tells us that neural networks can compute any function; and empirical evidence suggests that deep networks are the networks best adapted to learn the functions useful in solving many real-world problems.